Mathematical synchronization of image and sound in an animated film

Introduction

The precise synchronization of image and sound is the most important issue concerning the creation of films illustrated by the given music. Many authors synchronize image with sound by a time-consuming method of trial and error, often with a satisfactory result. However, we must keep in mind that there we may use more effective methods, based on the mathematical calculations. Music is a creative activity which is very easy to be put in mathematical formulae and numbers. The main field of musical activity which I would like to subject to the mathematical analysis is rhythm, as it can be easily divided into parts and assigned to the particular fragments of a film.

In order for the analysis to remain clear and comprehensible, I will explain the meaning of the musical and film abbreviations used throughout this article. The abbreviations provided in the table below were found in the sound and film editing computer programs.

B

ang. Beat, a single rhythmic beat – a part of the musical bar

T

ang. Tick, the smallest rhythmic unit – a part of the beat

F

ang. Frame

BPM

ang. Beats Per Minute

FPS

ang. Frames Per Second

TPB

ang. Ticks Per Beat

Let us now get a closer look at the particular synchronization techniques.

Adjusting the tempo of a musical piece to the standard FPS

The simplest means by which we may achieve considerably precise synchronization of the musical rhythm with image is the adjustment of the musical piece’s tempo, so that the smallest rhythmic unit corresponds with one or a few film frames. An example of such an animation synchronized with sound by this technique is “Mickey’s Choo-Choo” (©1929 Disney Studios). At that time, the standard frequency of film replay was 24FPS, as the tempo 90BPM suggests. Why? Let us look at the mathematical formula and its application below:

The number 16 substituted to TPB results from the division of the rhythmic beat into sixteen equal parts. It can be easily deducted from the calculation above that if every film frame must correspond with the sixteenth of the rhythmic beat at the frequency of 24FPS, the tempo of the musical piece must be 90BPM. Indeed, the music in the animation “Mickey’s Choo-Choo” has a constant tempo 90BPM. The adjustment of Mickey Mouse’s movement to music was probably based on the peculiar notation, in which it was easy to separate the rhythmic units corresponding with the individual film frames. What is more, the animation “Mickey’s Choo-Choo” is divided into equal parts, each one of them having the length which equals the multiple of 64 frames. The individual scenes of the animation correspond with the successive musical bars. Such a division makes the synchronization of musical phrases repeating in bars with image more comfortable.

We must remember that such a solution is natural, when the author of a film is an author of music at the same time or at least he or she has an influence on the creation of music to the film in question.

Adjusting FPS to the tempo of a musical piece

The situation becomes more difficult when the music is already prepared. Then we must calculate FPS ourselves so that the film frames correspond with the rhythmic divisions. However, before we do this, it is necessary to thoroughly analyze the rhythm appearing in a given musical piece. I suggest to divide the musical piece into logical parts as well (e.g. verses in the case of a song), since it will be needed to separate the musical bars in a film as well. Furthermore, some changes of rhythm and tempo, which must be taken into account in the animation, may occur in our musical piece. It is fairly simple if the music was produced by computer, because then the tempo should remain constant. When the music is created by people, slight imbalances of tempo are inevitable. One-percent tempo change is enough to result in a discrepancy between sound and image even up to one second. Therefore, we must measure the duration and tempo of each part of the musical piece. The tempo of a given piece expressed in BPM results from a following formula:

In order to perform the calculations more effectively, we may express this formula in a more practical way:

We may calculate FPS with BPM given before according to the following formula:

It is good to verify whether the calculations are correct. In order to do this, we should prepare a simple animation. For example, it may be one white frame at the beginning of each bar looped repeatedly throughout the whole musical piece. If the “twinkling” of the white frames matches the musical rhythm, this will mean that our attempt is successful.

Notation

After performing detailed calculations, it is time to analyze the individual sounds. In order to do this, I modify the given musical piece to maximally slow down its tempo. After that, I listen carefully and make notes. Thanks to this technique, I can prepare a notation similar to the one below: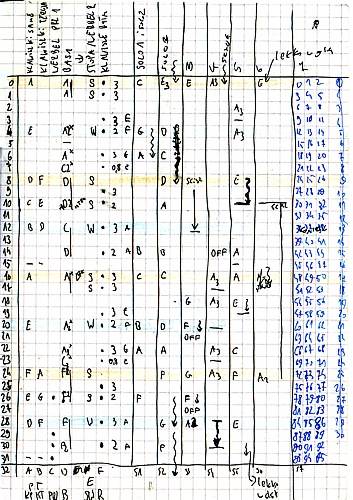

The transcription of sounds from the animation “My Jesus”

As we can see in the picture, each bar will consist of 32 frames. The next stage is the greatest fun. Bit by bit, we may draw what our imagination suggests for particular sounds and melodies.

Interpolation

After creating a series of short films for each part of music separately, there is a need to put all the elements together into one film and join it with sound. It is obvious that the finished film should have constant FPS, so we must standardize FPS in all separate parts, maintaining their previous durations at the same time. Therefore, the change of FPS is not enough – an interpolation of frames is necessary so that the time divisions stay unchanged. Additionally, it is good for the target FPS to be quite high, since the possible differences in the length of the frames caused by interpolation are smaller. Of course, FPS should also correspond with the standard – for example, in PAL system the frequency of 25FPS is used, which gives considerably good results in the case of 12FPS in an original animation.

Unfortunately, interpolation is connected with some inconveniences. First of all, the quality of the film decreases because of the repetition of the frames. Next, we cannot use the higher FPS frequency than the standard one, since some of the frames drawn simply will not appear in the film. Editing the scenes recorded with a video camera in this technique may also turn out to be problematic. The technique itself is simple, but there are situations in which it is not applicable.

The calculation of the frames

It is not necessary for all animation frames to match exactly the rhythmic divisions in music to achieve good synchronization. When we divide the rhythmic beat into sixteen parts, only in some of them there will be moments, which will have to be reflected by image. We may establish FPS right at the beginning according to the standard, and then calculate the numbers of the frames, referring to the musical rhythm. It is possible even when the tempo is changing throughout the song. An example of animation synchronized with sound in such a way is “Starship Groove” by Animusic. The tempo of the song is 111BPM, and the frame change frequency is 29,97FPS. How can we determine the numbers of the frames, having the tempo and FPS given before? The first thing we need to do is to calculate the duration of one beat in the frames, using the following formula:

In the case of the music from “Starship Groove” this calculation will look as follows:

Thus, one rhythmic beat will last exactly 16,2 frames. In order to achieve more clear-sighted synchronization, we may also divide this beat into, for example, sixteen parts. Thanks to such a division we know that the sixteenth of the beat will last 1.0125 of the frame. These values can be multiplied so as to receive the frame number for any frame, beat, or even sound. There is only one problem occurring: the numbers of the frames have fractional values. I suggest to round them down. Why down? The speed of light is much faster than the speed of sound – this is why we always see the image first, and then we hear the sound related to this image. If, according to the calculations, the important moment in the music falls, for example, on the frame number 372.6, after rounding this frame down we will obtain the frame 372. If we rounded the frame number up, we would hear it 0.4 of the frame (about 0.01 sec) before the image. Although the discrepancy between image and sound is smaller in the case of rounding up, the effect of synchronization will be slightly clearer in the case of rounding down.

Hypothetically, as far as this film is concerned, we could use the simpler method of synchronization as well, since the animation was created in 3D technology. As we know, the major part of the work related to generating such animations is performed by computers. Nothing stands in the way to generate the animation in 3D technology, using the higher FPS frequency than the standard one, and then to interpolate FPS to target values. Having the tempo 111BPM and the division of the rhythmic beat into 32 parts, we will obtain 59.2FPS. Therefore, after the interpolation almost the half of all frames will be lost, which does not mean that the graphic designers will have to work twice as long. Only the computers will “suffer the loss” of time.

Conclusions

There are many more methods of synchronization of sound and image apart from the ones introduced in this article. Human creativity is limitless, so plenty of other interesting solutions in this field are possible to be found. Let me summarize the ideas which I presented in this article:

Sincere thanks to:

• Wayne Lytle from Animusic studio (http://animusic.com) for permission to publish the fragment of one of his animations and some valuable remarks concerning synchronization
• musical band New Life’m (http://newlifem.com) for permission to use the musical piece “Wołam do Ciebie Panie” for the animation.

Bibliography

• http://en.wikipedia.org/wiki/Animated_cartoon
• Kevin Brownlow, Silent Films: What Was the Right Speed? (1980).
  http://www.cinemaweb.com/silentfilm/bookshelf/18_kb_2.htm